3 minutes
Tranposed Convolution
The transposed convolution is also called:
- Fractionally strided convolution
- Sub-pixel convolution
- Backward convolution
- Deconvolution (The worst name - it’s confused and shouldn’t be used at all)
If we unroll the input and output feature maps of a convolution operation into vectors from left to right, top to bottom, the convolution could be represented by a matrix multiplication with a spare matrix \(C\). For example, below is a spare matrix for a convolution with kernel size \(3\), stride \(1\), padding \(0\) over a \(4 \times 4\) input, resulting in a \(2\times2\) output.1

The convolution above transformed the \(16\)-dimensional vector into \(4\)-dimensional vector. With this representation, it’s easy that we can do the reverse transform, which is transforming a \(4\)-dimensional input to \(16\)-dimensional input while keeping the original connectivity pattern, with the help of the transposed matrix \(C^T\). This is the underlying principal of the transposed convolution - swapping the forward and backward pass of the normal convolution.
One way to think about transposed convolution is by multiplying the scalar in the input feature map with the kernel weights to create immediate results of the output feature map. The position of the immediate result depends on the position of the scale in the input feature map. The final output is the sum of all immediate results.2.
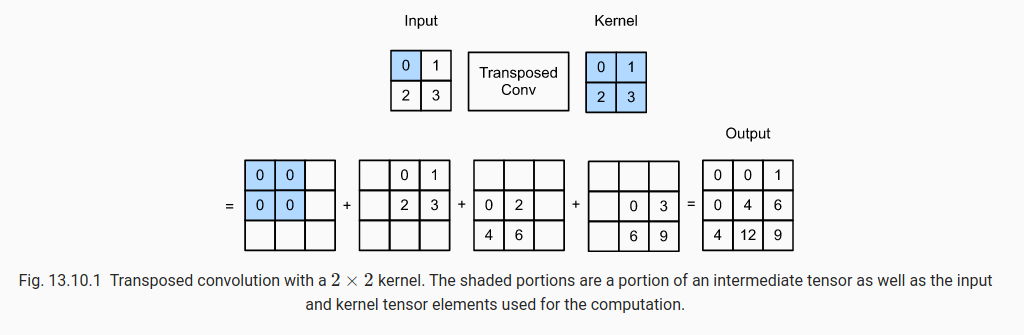
Another way to think about transposed convolution is to apply an equivalent - but much less efficient - direction convolution on input feature map. Imagining the input of transposed convolution being the result of a direction convolution applied on some initial feature map, the transposed convolution can be considered as the operation that recovers the shape of this initial feature map.1 This way of thinking is reasonable because the transposed convolution is the just backward pass of a direction convolution.
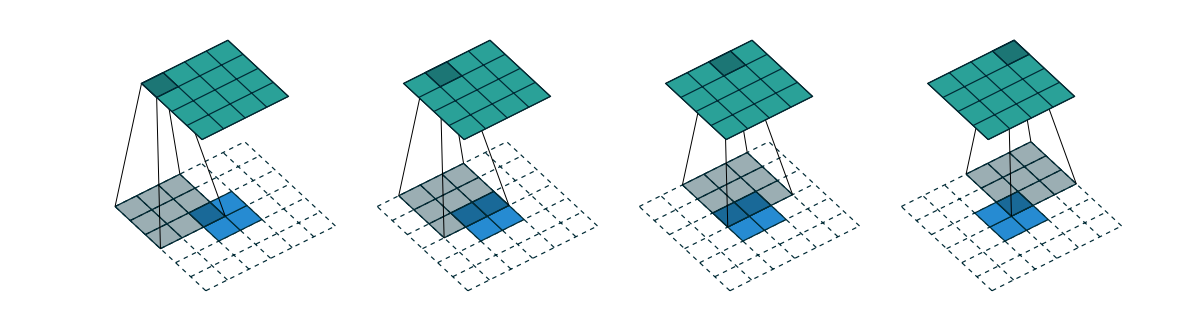
In addition, considering transposed convolution in its relation to a direction convolution gives rise to the relationship between two convolution operations. Given a direct convolution with kernel size \(k\), stride \(s\), padding \(p\), the transposed convolution has the same kernel size \(k' = k\), stride \(s' = 1\) (noted that the stride for convolution of transposed convolution always has stride \(1\)).
- When \(p = 0\) (no padding) and \(s = 1\), considering the top left pixel of input of normal convolution, it only contributes to the top left pixel to the output. Therefore, for transposed convolution to maintain this connectivity pattern, it’s necessary to add zero padding around the input of transposed convolution. The padding for transposed convolution’s input is \(p'=k-1\).
- When padding is used in the normal convolution, it’s reasonable to see that we need to reduce the padding of the transposed convolution. This can be explained by the observation that the top-left pixel of the original input (before padded) now contributes to more pixels output. The new padding for transposed convolution’s input is \(p' = k - 1 -p\)
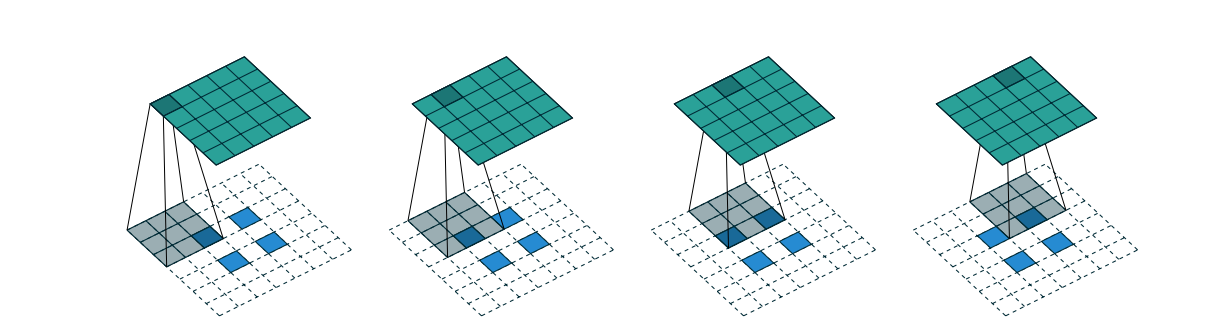
- When stride \(s > 1\) is used for normal convolution, the intuition for transposed convolution is to make the sliding window moves slower. This is made possible by adding zero pixels between actual pixel in the input. For normal convolution with stride \(s\), \(s-1\) zero pixels are added between actual in the input. This is where the name fractionally strided convolution comes from. Strided transposed convolution is commonly used to increase the spatial size of feature map.
-
A guide to convolution arithmetic for deep learning ↩︎
-
https://d2l.ai/chapter_computer-vision/transposed-conv.html ↩︎